黄金分割率广泛存在于各个领域内，外汇期货股票等交易市场中的黄金分割率理论就是以神奇的黄金分割为核心的。那么，什么是黄金分割率呢?
一般地，我们称0.61803398……为黄金分割数。黄金分割数的历史远比斐波那契数列来得悠久。在古希腊，公元前6世纪，毕达哥拉斯学派就研究过正五边形和正十边形，这些正多边形与黄金分割关系极为密切。他们还发现，音阶也跟黄金分割有关。因此人们猜测，毕达哥拉斯学派已经了解了黄金分割方面的知识。公元前4世纪，大数学家欧多克斯在研究比例问题时，也注意到了黄金分割。
公元前3世纪问世的堪称“数学第一书”的《原本》，也是第一部流传至今的提到黄金分割的著作。在其第2篇中提到，分已知线段为两部分，使它与其中一条线段所构成的矩形面积等于另一条线段为边长的正方形面积，在几何上就是将线段分成“中外比”，后来叫做“黄金分割”。欧几里得在论述立体几何时，也不时提到黄金分割。可见，当时的古希腊人已非常重视这个比例。
雅典有座大理石砌成的神庙，其中有一尊雅典娜神像，由象牙和黄金雕制而成，姿态优美。研究发现，雕像从肚脐到脚底的距离与身高的比值约等于0.618。芭蕾舞演员虽然身材修长，但该比值平均约为0.58，只有在踮起脚尖时才能提高这个比值，展现0.618的魅力。报幕员在报幕时，往往不会站在舞台正中，而是站在舞台的黄金分割点上，以便给观众留下更协调的印象。正五角星中也蕴含着黄金比：正五角星的每条边恰好被与之相交的另外两条边黄金分割。
首次将这种比例冠以“黄金”美称的是达·芬奇。在“现代会计之父”帕乔利（L．Pacioli）的《神奇的比例》一书中，达·芬奇作了插图，
还对各种图形中的黄金分割数作了精彩的描述。比如，将3个黄金矩形对称地互相交叉，每个都与另外两个垂直，则这三个矩形的顶点恰好是一个正二十面体的12个顶点，也是一个正十二面体的各个面的中心。
稍后的德国著名科学家开普勒对黄金分割也极为着迷，他曾经说道：“几何学有两大财富：一个是毕达哥拉斯定理（勾股定理），一个是按中外比划分一条线段。第一大财富可称得上是黄金定理，第二大财富称得上是珍珠定理。”最早明确使用“黄金分割”这一名称的是德国数学家M．欧姆（M．Ohm），他是发现电学欧姆定律的欧姆（C．S．Ohm）的弟弟。在著作《纯粹初等数学》（1835年）中，他用“黄金分割”来表述中外比，后来这一称呼就逐渐流行起来。
20世纪中叶，美国数学家巴尔（M．Barr）给比率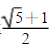 
起名为Φ（也有人写作φ，读作Phi），这是古希腊雕塑家菲迪亚斯（Phidias）名字的第一个字母。但是，这一称呼并没有像π和e一样得到数学家的公认。另外，也有不少人用τ表示黄金分割数。
在达·芬奇的名画《维特鲁威人》中，人体比例的确定也与黄金分割息息相关。画名取自古罗马杰出的建筑师维特鲁威（Marcus Vitriivius Pollio）之名。这位建筑师在他的著作《建筑十书》中曾盛赞人体比例和黄金分割。我们前面提到过的小说《达·芬奇密码》中，馆长临死前全身赤裸，把自己摆成画作《维特鲁威人》中的形象，为破案提供了线索。现代西班牙超现实主义画家达利（S．Dali）的《最后的圣餐》，也是画在一个黄金矩形（长和宽之比为黄金分割数的矩形）上的。在给人物定位时，达利还采用了另一些黄金矩形，而画作的顶端则是一个巨大的正十二面体的一部分。
1939年，艾略特（R．N．Elliot）发现了斐波那契数列与股市的关系。他提出著名的“艾略特波动原理”，指出股票的变化是一个个“小周期”的不断重复：牛市和熊市被最大的波动分成2（=1＋1）部分；而第二波（较大的波动）中，牛市共有5个，熊市则有3个；第三波（中等大小的波动）中，牛市共有21个，熊市则有有13个；第四波（小波动）中，牛市、熊市分别有89和55个。于是有人戏称，要想赚钱，还得弄懂斐波那契数列。
黄金分割律还为最优化方法的建立提供了依据。假设在区间[0，1]上有一个连续函数f(x)，它只有一个最大值f（x0），如何求出这个x0呢？这个问题具有非常大的实用价值，但f（x）往往没有表达式和具体图象，因此需要寻找一种方法进行搜索。“二分法”是首选，即寻找中点，再在剩下的区间分别找中点，如此一直继续下去，把不是最大值的点逐一淘汰。但是对分法的计算量太大。如果将实验点定在区间的黄金分割点，那么实验的次数将大大减步。实验统计表明，用“0.618法”做16次实验，就可取得“对分法”做2500次试验所达到的效果。1953年，美国的基弗（J．Kiefe。）提到“0.618法”已经被大量应用于生活中，特别在工程设计方面。中国著名数学家华罗庚成功地在中国推广了“0.618法”。
暂无评论内容